Nitrogen-Phytoplankton-Salinity MATLAB Example
MATLAB is a popular script-driven computing environment for doing ocean science data analysis. Below is an example of a MATLAB script, using a Nitrogen-Phytoplankton-Salinity (NPS) model as an example. Compare the MATLAB script with the Python script to see the differences in approach. The MATLAB script is shown here:
%Advection Diffusion Lab
%Explore the movement of salt in a shallow estuarine channel
%1 April 2011 MH
clear all
close all
fr = 1;
%Define the Parameters (be sure to convert lengths to cm) UNITS!!!
L=2e6; %length of estuary (20 km)
h=1.5e3; %depth of estuary (15 m)
dx=5e4; %horizontal grid spacing (0.5 km)
dz=1e2; %vertical grid spacing (1 m)
Kh=1e6; %horizontal diffusivity (10^5 cm^2/s)
Kv=0.110; %*a vertical diffusivity (try two values: 0.1 and 10 cm^2/s)
B0=3e-5; %*b applied pressure gradient (try three values: 7e-5, 0, -7e-5 cm^2/s)
Mu=1; %dynamic viscosity (g/(cm*s))
Uo=8; %applied surface velocity (cm/s)
Vm=0.025;
Vm=0.000125; %growth rate in inverse seconds
Cmax=5.0;
tideamp=10.0;
Ks=1.0; %half saturation coefficient
%Set up time and nodes
dt=200;
X=0:dx:L;
Z=0:dz:h;
Ntimes=2500;
nz=h/dz+1;
%Set up plot parameter for velocity field
xV=linspace(0,L,10);
zV=linspace(0,h,10);
[XV,ZV]=meshgrid(xV,zV);
Uv=zeros(size(XV));
utS=zeros(Ntimes);
utB=zeros(Ntimes);
utt=zeros(Ntimes);
%Set up salinity matrix
S=zeros(h/dz+1,L/dx+1,Ntimes);
%Initial salinity
S_initial=linspace(5,30,L/dx+1);
for i=1:h/dz+1
S(i,:,1)=S_initial;
end
%Boundary Conditions
S(:,1,:)=5;
S(:,L/dx+1,:)=30;
%Initial concentration
C_initial=linspace(Cmax,0,L/dx+1);
P_initial=linspace(0,0,L/dx+1);
for i=1:h/dz+1
C(i,:,1)=C_initial;
P(i,:,1)=P_initial;
end
%Boundary Conditions: depth, distance, time
C(:,1,:)=Cmax;
C(:,L/dx+1,:)=0;
P(:,1,:)=0;
P(1:6,L/dx+1,:)=5;
P(7:h/dz+1,L/dx+1,:)=0;
%Calculate the average flux of a day
sumU=zeros(size(Z));
Lp3=floor((L/dx)/3);
Lp6=floor((L/dx)*2/3);
averageU=sumU/(24*3600);
xlabel('Velocity(cm/s)')
ylabel('Depth(cm)')
B=B0;
Ures=(0.5*B/Mu).*Z.^2+((Uo/h)-(0.5*B*h/Mu)).*Z;
%Calculate salinity over time
for k=2:Ntimes-800 %TIME
%B=B0*sin(k*dt/(24*3600)*2*pi);
utide=tideamp*sin(k*dt/(12*3600)*2*pi);
U=Ures+utide;
utS(k)=U(14);
utB(k)=U(4);
utt(k)=(k*dt)/(3600*24);
velocityh=(0.5*B/Mu).*zV.^2+((Uo/h)-(0.5*B*h/Mu)).*zV;
velocityh=velocityh';
Uh=repmat(velocityh,1,10);
C(:,1,k)=5;
P(1:6,L/dx+1,k)=5;
for j=2:L/dx %LENGTH
for i=2:h/dz %DEPTH
Nsrc=Vm*(C(i,j,k-1)/(Ks+Cmax))*P(i,j,k-1)*(i/(h/dz))*dt;
if U(i)>0
S(i,j,k)=S(i,j,k-1)-U(i)*(dt/dx)*(S(i,j+1,k-1)-S(i,j,k-1))+Kh*(dt/dx^2)*(S(i,j+1,k-1)-2*S(i,j,k-1)+S(i,j-1,k-1))+Kv*(dt/dz^2)*(S(i+1,j,k-1)-2*S(i,j,k-1)+S(i-1,j,k-1));
C(i,j,k)=C(i,j,k-1)-U(i)*(dt/dx)*(C(i,j+1,k-1)-C(i,j,k-1))+Kh*(dt/dx^2)*(C(i,j+1,k-1)-2*C(i,j,k-1)+C(i,j-1,k-1))+Kv*(dt/dz^2)*(C(i+1,j,k-1)-2*C(i,j,k-1)+C(i-1,j,k-1));
P(i,j,k)=P(i,j,k-1)-U(i)*(dt/dx)*(P(i,j+1,k-1)-P(i,j,k-1))+Kh*(dt/dx^2)*(P(i,j+1,k-1)-2*P(i,j,k-1)+P(i,j-1,k-1))+Kv*(dt/dz^2)*(P(i+1,j,k-1)-2*P(i,j,k-1)+P(i-1,j,k-1));
C(i,j,k)=C(i,j,k)-Nsrc;
if C(i,j,k) < 0.0 ;
C(i,j,k)=0.0;
end
P(i,j,k)=P(i,j,k)+Nsrc;
else
S(i,j,k)=S(i,j,k-1)-U(i)*(dt/dx)*(S(i,j,k-1)-S(i,j-1,k-1))+Kh*(dt/dx^2)*(S(i,j+1,k-1)-2*S(i,j,k-1)+S(i,j-1,k-1))+Kv*(dt/dz^2)*(S(i+1,j,k-1)-2*S(i,j,k-1)+S(i-1,j,k-1));
C(i,j,k)=C(i,j,k-1)-U(i)*(dt/dx)*(C(i,j,k-1)-C(i,j-1,k-1))+Kh*(dt/dx^2)*(C(i,j+1,k-1)-2*C(i,j,k-1)+C(i,j-1,k-1))+Kv*(dt/dz^2)*(C(i+1,j,k-1)-2*C(i,j,k-1)+C(i-1,j,k-1));
C(i,j,k)=C(i,j,k)-Nsrc;
if C(i,j,k) < 0.0 ;
C(i,j,k)=0.0;
end
P(i,j,k)=P(i,j,k-1)-U(i)*(dt/dx)*(P(i,j,k-1)-P(i,j-1,k-1))+Kh*(dt/dx^2)*(P(i,j+1,k-1)-2*P(i,j,k-1)+P(i,j-1,k-1))+Kv*(dt/dz^2)*(P(i+1,j,k-1)-2*P(i,j,k-1)+P(i-1,j,k-1));
P(i,j,k)=P(i,j,k)+Nsrc;
end
end
end
S(1,:,k)=S(2,:,k); %depth, dist, time
S(end,:,k)=S(end-1,:,k);
for i=2:nz-1
if U(i)>=0
S(i,end,k)=S(i,end-1,k);
else
S(i,end,k)=30.0;
end
end
P(1,:,k)=P(2,:,k); %depth, dist, time
P(end,:,k)=P(end-1,:,k);
C(1,:,k)=C(2,:,k);
C(end,:,k)=C(end-1,:,k);
if (k>=100 & mod(k,60)==0)
figure(1)
box('on');
hold('all');
subplot(3,1,1)
pcolor(S(:,:,k));
shading interp
caxis([0 30])
text(30,20,['Time is ' num2str(k*dt/3600) 'hours'] );
title('Salinity','FontSize', 18);
subplot(3,1,2)
pcolor(C(:,:,k));
shading interp
caxis([0 5])
title('Nitrogen' ,'FontSize', 18);
ylabel('Height above bottom,m','FontSize',11)
subplot(3,1,3)
pcolor(P(:,:,k));
shading interp
caxis([0 5])
xlabel('Distance along West Passage,km','FontSize',11)
title('Phytoplankton','FontSize', 18);
pause(.01)
M(fr) = getframe(gcf);
fr = fr+1;
clf('reset')
end
end
movie2avi(M,'lab10_np','FPS',1) %make an AVI movie from timestep plots
The script runs through MATLAB application software. Open a script file (they normally have a .m extension) and click on the Run button:
With MATLAB, all loaded modules are available for use in the script. You can determine which modules load when you launch the MATLAB program.
I probably have overdone it as MATLAB takes a while to load as a result of all the modules it readies at launch time. I am only using about 2% of them in
the script. When you run a script within MATLAB, you can run one line at a time (like the control we
have over using Python in a Jupyter notebook). After each timestep loop in the model, a figure dialogue window shows the result.
26.67 hours into the simulation, the figure dialogue window shows:
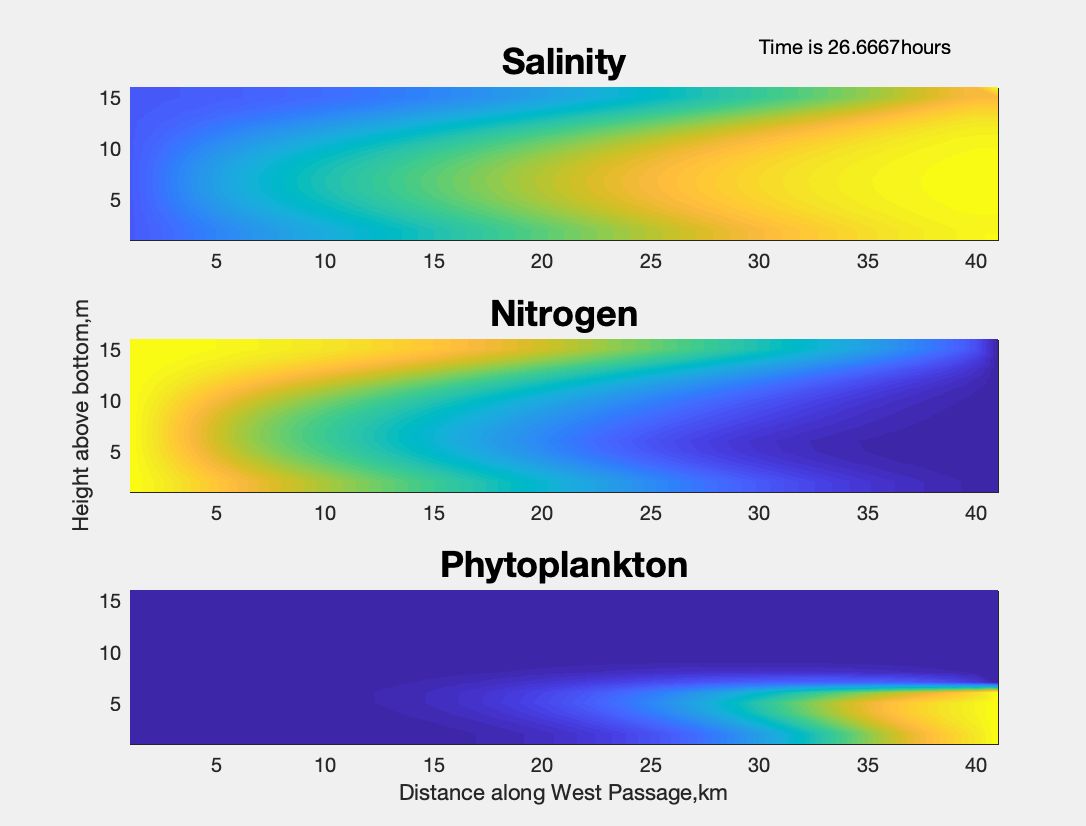
The plotting interface in MATLAB is straight-forward and similar to the Matplotlib services interface in Python.

